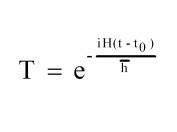Symmetry & Measurement

Measurement in terms of units

“The formulation of the fundamental laws of nature requires the mathematics of transformations.

The important things in the world appear as the invariants … of these transformations.

Further progress lies in the direction of making our equations invariant under wider and still wider transformations.” [Dirac]

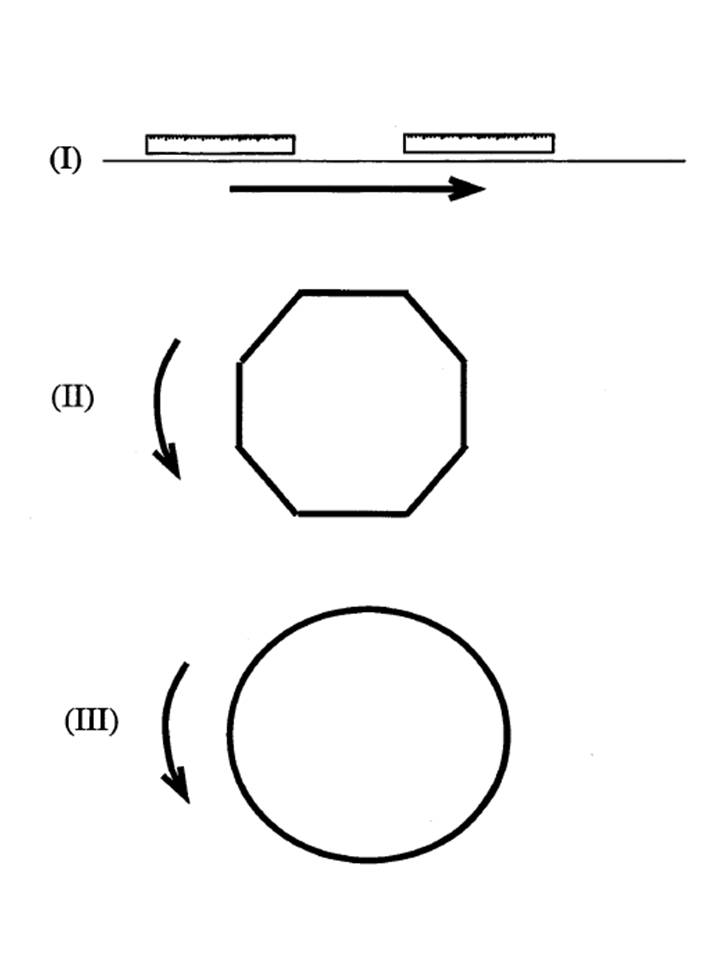
Symmetry_ Measurement
Symmetry & Measurement Units
  • displacing a standard (a measuring stick, for example, with which the unit is realised)
  • counting the number of times the standard fits into the measured interval.

Key assumptions:

  • measuring standard does not change when being displaced
  • space is symmetric with respect to displacements in that particular dimension.

It is easy to see for most measurement units that they are associated with symmetry in this way.

Use of units => measurement process in terms of symmetry transformations.

Isolated systems. Standards of frequency and length

Number of physical quantities known by experiment to be conserved in an isolated system:

  • total energy, momentum, angular momentum remain constant,
  • whatever and however complex interactions occur within the system.

consequences of invariance of mechanical systems under changes of time, under length translation and under rotation in space, together with the principal of least action Landau and Lifshitz.

Isolated system => prime candidate as measurement standard

  • Variables canonical with energy and momentum, namely time and (linear and angular) position.
  • Periodic (i.e. symmetric) behaviour of intervals in these dimensions allows the identification of standards of frequency and length.
– both for classical mechanical systems as well as relativistic and quantum mechanical systems.

Dirac [Principles of Quantum Mechanics]

Number of unitary transformation operators for conserved physical quantities, for example

Unitary transformation

for time and energy, with associated stationary states.

Translational symmetry and fundamental quantum condition => eigenvalues expressed as integer (or half-integer) multiples of Planck constant, ħ , the measurement unit of quantum mechanics.

Interacting systems. Standards of mass and charge

Total energy of physical system = kinetic + potential energies

Kinetic energy ≈ velocity^2

  • constant of proportionality = inertial mass

Potential energy of two interacting systems ≈ (inverse) distance between them

  • constant of proportionality = product of ‘charges‘

Fundamental fields of interaction

  • electromagnetic, weak, strong and gravitational.

NB: gravitational mass, ‘charge’ – distinct from inertial mass

Current theories of nature of physical world

  • identify some fundamental and universal symmetries,
  • all of which can have measurement units associated with them in the most fundamental way, expressed as fundamental constants.

Examples are:

  • relativistic Lorentz invariance => c speed of light
  • Gauge invariance of electromagnetic interaction => e, elementary charge (of electron, proton, etc)
  • Grand unified gauge invariance => α, fine structure constant for all fundamental interactions (electroweak and strong) excepting gravity.

___________________________________________________

Links

Leave a comment